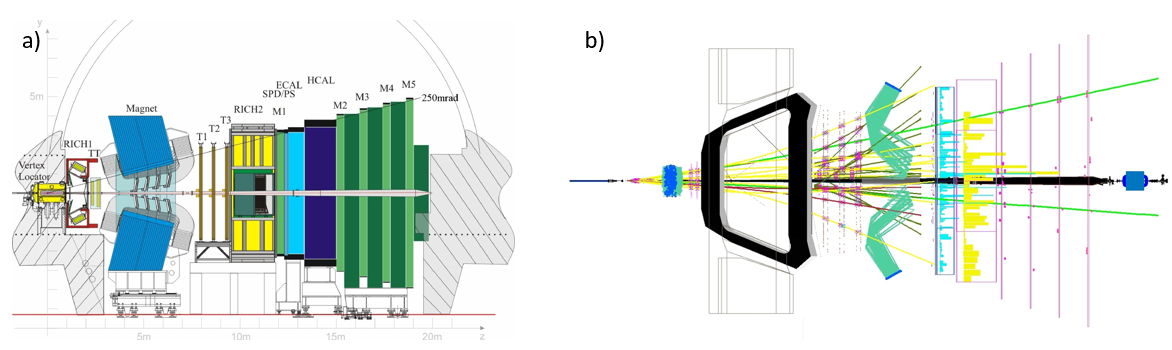
The LHCb Detector and the Data
The LHCb detector is a single-arm forward detector that covers the pseudo-rapidities between $2<\eta<5$. Originally, it was designed for the study of particles that contain $b$ or $c$ quarks. The detector schematic is presented in Fig. 2a). Following this schematic, the various parts of the detector are described below.
The LHCb detector includes a tracking system made from a silicon-strip vertex detector surrounding the interaction point (VELO), a large silicon detector (TT), a dipole magnet with a bending power of $\sim 4$ Tm, and three stations of silicon-strip detectors and straw drift tubes representing the outer tracker (T1, T2, T3). Trackers enable physicists to measure the trajectory of each particle passing through the detector. The VELO, which is placed close to the beam pipe, uses silicon microstrip detectors to record the paths of particles going through it and is especially important in distinguishing $B$ mesons from the $pp$ interaction point, as the former fly distances of $\sim 1$ cm. Charged particles collide with silicon atoms and thus free electrons, which in turn create an electric current that traces the path of the original particle. The outer tracker is situated further from the beam pipe and is made up of thousands of gas-filled straw tubes. When a charged particle passes through, it ionizes the gas, producing electrons. The position of the track is determined by measuring the time taken for the electrons to reach the central anode wire of their respective tube. The asymmetries in the detection efficiency due to nonuniformities in the detector response are reduced by periodically reversing the polarity of the magnet while taking data. Particles normally travel in straight lines, but the presence of a magnetic field curves the paths of charged particles, with positive and negative particle trajectories being bent in opposite directions. The curvature of the path can be analyzed to obtain the momentum of the particle, thus working towards establishing its identity. The tracking system measures the momentum $p$ of charged particles with very high precision, giving a relative uncertainty that varies from 0.5% at low momentum to 1.0% at high $p$. The impact parameter (IP), which is the minimum distance of a track to its vertex of origin, is measured with a high resolution.
The charged hadrons are identified using the two ring-imaging Cherenkov (RICH1 and RICH2) detectors. RICH detectors work by measuring Cherenkov radiation. This type of radiation is produced when a charged particle passes through a certain medium, in this case a dense gas, faster than light does. In its path, the particle emits a cone of light which is reflected by mirrors built into the RICH detector onto an array of sensors. The shape of the cone of light depends on the particle’s velocity and thus its speed is determined. This additional bit of information is then combined with the particle trajectory, recorded using the tracking system, to determine its mass, its charge, and finally, its identity. The RICH detectors can identify the various charged particles resulting from the decay of $B$ mesons, such as pions, kaons, and protons.
Furthermore, final state particles such as photons, electrons, and hadrons are distinguished by a calorimeter system which consists of the scintillating-pad and preshower detectors (SPD), an electromagnetic calorimeter (ECAL) and a hadronic calorimeter (HCAL). The calorimeter system is designed to stop particles as they pass through and thus measure the amount of energy lost as a particle comes to a halt. The ECAL is responsible for determining the energy of lighter particles, such as electrons and photons, while the HCAL measures the energy of protons, neutrons, and other particles that contain quarks. Both calorimeters consist of alternating layers of metal and plastic plates. Relatively heavy particles produce showers of secondary particles as they hit these metal plates. In turn, the showers excite molecules in the plastic plates, which then emit ultraviolet (UV) light. The amount of UV produced is proportional to the energy of the particles that entered the calorimeter system. Calorimeters are crucial in identifying particles that possess no electrical charge, such as photons and neutrons.
Muons are present in the final stages of many $B$ meson decays and thus their detection is important for LHCb. Muons are measured by a system of alternating layers of iron and multiwire proportional chambers (M). Located at the far end of the detector, the muon system includes five rectangular stations, which increase in size. Each station has chambers filled with a three gas mixture; muons ionize the gases and electrodes record the products. This works on the same principle as the tracker.
Once a signal is recorded in the physical detector, a selection is applied by a trigger system while still actively taking data. The LHCb trigger is essential in selecting the collisions of interest for $B$ meson studies from all the recorded events. The trigger is based on a two level system and exploits the fact that hadrons containing the $b$ quark are relatively heavy and long lived. The selection consists of a hardware stage, based on the calorimeter and muon system responses, and a software stage, which facilitates the complete event reconstruction. A full event reconstruction culminates as exemplified in Fig. 2b), and the decay data is saved for further analysis. To pass the hardware stage, events require a high transverse momentum ($p_\mathrm{T}$) muon to be detected in the muon chambers or a high energy hadron, photon, or electron to be detected in the HCAL or in the ECAL. The software trigger requires the existence of an up to four-tracks secondary decay vertex with a high $p_\mathrm{T}$ sum and a significant displacement from the primary IP. Thus, at least one track should posses a $p_\mathrm{T}$ of about 1 GeV and a relatively high $\chi^2_\mathrm{IP}$, where $\chi^2_\mathrm{IP}$ is the difference in the $\chi^2$ of a primary vertex fit that has original particle reconstruction being applied and a fit that was performed without using the reconstruction information.
As mentioned in the introduction, the processes of interest are $B^+\rightarrow D^{(*)+}\bar{D}^0$ and $B^+\rightarrow D_s^+\bar{D}^0$, with the subsequent decays: $\bar{D}^0\rightarrow K^+\pi^-$, $\bar{D}^0\rightarrow K^+\pi^-\pi^+\pi^-$, $D^+\rightarrow K^-\pi^+\pi^+$, $D^+_s\rightarrow K^+K^-\pi^+$, and $D^{*+}\rightarrow D^0\pi^+_s$. These subdecays are reconstructed in the LHCb detector as outlined in the previous paragraph; a more in-depth explanation of the trigger system in the context of the studied decays is found in Alison’s Thesis and is beyond the scope here. After passing the trigger selection, the event is stored on disk and is in principle ready for offline analysis. However, other selection cuts are often made before an analysis is performed on the data. Thus, a broad selection is applied on the raw trigger information, to construct a proper data set on which, say, a $CP$ asymmetry measurement can be performed.
The data samples for this analysis are the refined Run~I and Run II data sets collected by the LHCb experiment. This refinement was performed in two steps. First, a centralised preselection was used, also known as stripping. The stripped data sets were obtained by applying a number of loose requirements to select the particular decay channels of interest. Then, a momentum scale calibration was applied to account for the possible momentum measurement bias due to imperfect knowledge of the magnetic field in the tracker. Secondly, a further preselection, detailed in Ch. 4.6 of Alison’s Thesis, is performed to reduce the background levels with little loss of signal.
Simulated particle decay samples, known as Monte Carlo data sets, were quintessential for this measurement, since they were used for the training of the multivariate selection algorithm, and for constraining the signal shapes of the invariant mass fits. These simulations model $pp$ collisions in which the studied decays were then generated. All known issues regarding the simulation, including the mass scale, momentum resolution, and the RICH response, were corrected through data-driven methods. The MC data was compared to the actual data and validated.